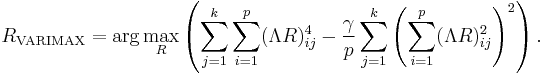Varimax rotation

In statistics, a varimax rotation is a change of coordinates used in principal component analysis and factor analysis that maximizes the sum of the variances of the squared loadings. That is, it seeks a basis that most economically represents each individual—so that each individual can be well described by a linear combination of only a few basis functions:

R_\mathrm{VARIMAX} = \operatorname{arg}\max_R \left(\sum_{j=1}^k \sum_{i=1}^p (\Lambda R)^4_{ij} - \frac{\gamma}{p} \sum_{j=1}^k \left(\sum_{i=1}^p (\Lambda R)^2_{ij}\right)^2\right).

where γ = 1 for VARIMAX.

Suggested by Henry Felix Kaiser in 1958,[1] it is a popular scheme for orthogonal rotation which cleans up the factors as follows: "for each factor, high loadings (correlations) will result for a few variables; the rest will be near zero."

Varimax rotation is often used in surveys to see how groupings of questions (items) measure the same concept.

The advantages and disadvantages of the technique are discussed at the website of Columbia University [2].

Contents

Rotation in factor analysis

A summary of the use of varimax rotation and of other types of factor rotation is presented in this article on factor analysis.

Implementations

In the R programming language the varimax method is implemented in the GPArotation library by Coen Bernaards and Robert Jennrich.

See also

Notes

  1. ^ Henry F. Kaiser (September 1958). "The varimax criterion for analytic rotation in factor analysis". Psychometrika 23 (3). doi:10.1007/BF02289233. 
  2. ^ "Singular Value Decomposition". http://ingrid.ldeo.columbia.edu/dochelp/StatTutorial/SVD/. Retrieved 20 September 2008. 

External links

 This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.